Techniques for Sudoku-X, Jigsaw, Windoku, Gatai...

Pointing Pairs / Triples ... alias Common Peer Elimination, Simple Cross Over

This is similar to the Intersection for some variants. In this Diagonal Sudoku, the 9 of D\ is locked in R1C1,R4C4. Whichever the case, R1C4 cannot be 9 (nor could R4C1).

Here is a Pointing Triple. In this Diagonal Sudoku, the 4 of D\ is locked in R1C1,R5C5,R9C9. Whichever the case, R1C9 cannot be 4 (nor could R9C1).

This solver is extended for Killer Sudoku

Generalized Naked Subset

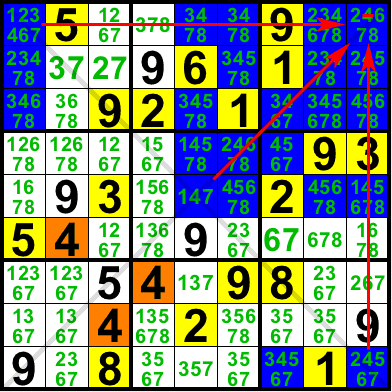
This is a generalization of the Naked Subset for some variants like Diagonal Sudoku. In this Diagonal Sudoku, R1C19,R9C9 forms a generalized naked triplet on {678} since each of the three cells is a buddy of the other two as shown by the blue lines: either through R1, C9 or D\. Since R9C1 is a buddy of all these three cells as shown by the red arrows, it cannot contain {678} (nor could R5C5).

This solver is extended for Killer Sudoku

Mandatory Inclusions

This solver for killer sudoku is also applicable to variants with partial / incomplete houses like Bold X, Large X, Snowflake, Argyle. It searches for Intersections of houses (nonets, extra groups...) locked within a partial / incomplete diagonal. As a result, the diagonal must include the locked candidate(s) and may play a role for pointing cells or strong links.

Twin Nonets

This is a particular case of Law of Leftovers applicable to some Gattai, overlapping grids. See Sudopedia for details.

Law of Leftovers (LoL)

This is a technique for Jigsaw and other grids with extra houses. It is also applicable to Cages 45/9 in Killer Sudoku.

Consider the two columns at the left of this puzzle. Each of them contains each digits 1..9.
Now subtract R8C2 and add R1C3.
This covers the two blocks/nonets at the left which also contains each digits 1..9.
Therefore these two cells must have the same value : R1C3 = 3

This can also be viewed in a way silimar to innies/outies of killer sudoku, considering blocks/nonets just like cages of 9 cells adding up to 45 :
Add all cells in the two blocks/nonets. The sum is 2*45 = 90.
Subtract all cells in C12. The sum is 90 - 2*45 = 0.
R1C3 is an outies, R8C2 is an innies : R1C3-R8C2 = 0 -> R1C3 = R8C2

Even if we don't know any fixed value of the cells, we may restrict their possibilities since they must have the same value.
For instance, if one cell were {1234} and the other were {3456}, we can deduce that each of them is either {34} :
The first cell cannot be {12} since the second cannot be {12}. The second cell cannot be {56} since the first one cannot be {56}.
The set of possible values is thus the intersection of all possible values for each half.

This may be extended to more cells.
Each half of the 4 cells in green must include the same set of 4 values : {R1234C9} = {R789C8+R9C7}
This means the set of 4 values in R1234C9 must equals the set of 4 values in R789C8+R9C7
We can deduce there must be a 4 in R1234C9 since R8C8 = 4
We may also deduce that none of the cells in green may have {17} since {17} are excluded from at least one half.

This may be used on more than two blocks/nonets.
Each half of the cells in red must include the same set of 3 values : {R389C5} = {R4C7+C5C67}
Although R3C5 and R89C5 are in a different blocks/nonets, they are in the same column, therefore no digit may be repeated in these.
The 4 is already located in both half
We can deduce the other two cells in each half must contain the same set (pair) of value : {R38C5} = {C5C67}
Since R38C5 cannot have a 5, R5C67 cannot have a 5 either. Which reveals that R5C3 = 5
Since R5C67 cannot have a 1, R38C5 cannot have a 1 either. Which reveals that there must be a 1 in one of R27C5

Here is a more complex use of LoL where some half contains cells which are not buddies of each other. In other words where numbers may usually be repeated.

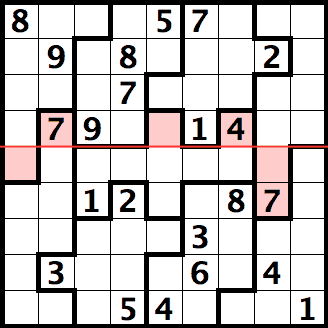
In this example, {R4C257} = {R5C1+R56C8}
Since no number may be repeated in {R4C257} -> no number may be repeated either in {R5C1+R56C8}, even if R5C1 could theorically hold the same value as R6C8.

More generally, every inference made for one half holds true for the other half. Some examples: If some candidate for some house is locked in one half, it is also locked for the other half. If one half forms an ALS, so does the other half. If one half of a jigsaw killer contains a cage 5/2 = {14|23}, it must hold one of {12}. So does the other half of the LoL. This kind of link is currently not detected by JSudoku.

LoL Synchronization

This solver updates / synchronizes the LoL sets previously found by the Law of Leftovers. It searches candidates missing in one half and removes them from the other half.

Hidden Extra Group

This solver uses the same pinciple as Killer Innies, but for Jigsaw using difference of rows (or columns) and blocks instead of cages. It is disabled by default since it is usually not productive and may slow down the solving process.

Note: Windoku already have all their 5 "hidden" windows defined. These are not displayed, but present as you can see by selecting them in the cell contextual popup menu.